
お断り
この記事は『ナンバーズの必勝法』とかの類ではなく、関連数字や組み合わせ・確率について見ていくというものです。
ナンバーズについて
個人的にナンバーズは好きでよく購入しています。
今回はそんなナンバーズに関する数字、組み合わせ、確率などについて見ていきたいと思います。
ナンバーズの概要
自分で細かく記載しようとも思いましたが、結構量が多くなりそうなので、確認されたい方はこちら(みずほ銀行「ナンバーズの特徴」)を参照願います。
これまでの実施回数
ナンバーズは2023年10月25日時点で6,327回実施されています。
宝くじ全体のお金
販売額
ナンバーズは年末年始を除く月~金まで販売されており、最近の1回あたりの販売額はおおよそ下記の様になるかと思います。
| くじの種類 | おおよその販売額 |
|---|---|
| ナンバーズ3 | 約8千万~9千万円/回 |
| ナンバーズ4 | 約2億円/回 |
当せん金・収益金・運営費の割合
販売額すべてが当せん金に回される訳ではなく、下記の様な割合で分配されている様です。(これは、ナンバーズに限らず、自治体発売の宝くじはだいたい同じ様です)
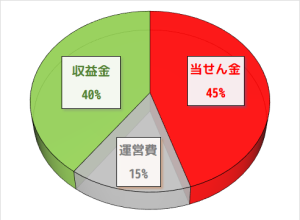
「当せん金」は当せん者へ分配されるものです。45%を多いと取るか、少ないと取るかは人によるでしょう…。
「運営費」は「印刷費・広報費・売りさばき手数料等」(宝くじの仕組みより)との事です。
「収益金」は販売元の自治体に納付されるものです。こちらは各自治体に割り振られ様々な事に用いられているようです。(「宝くじ号」と書かれた献血車はよく見ますね)
「収益金が多いな…」とも思うかも知れませんが、このおかげで当せん金が非課税になっているかも知れませんし、地方自治体の役に立っていると思えば…^^;
くじ全体としての期待値
販売額の45%が当せん金として支払われる訳なので、1口200円で購入したナンバーズの期待値は購入金額の45%の90円という事になります。
「期待値」が90円であっても、90円が必ず戻ってくる訳ではないですが…。
ナンバーズ3のミニを例に挙げると「00」~「99」まですべての組み合わせを1口ずつ100口購入するとその中の1枚は必ず当たります。
その時、購入費用は20,000円、当せん金は約9,000円(回によって異なる)となるので、
9,000 ÷ 20,000 = 0.45
となり、期待値通りになりますね…。
抽せん番号の決定
抽せん場所
東京や大阪の宝くじドリーム館で抽せんされます。
抽せん回数
年末年始などを除き、毎週月~金で実施されています。
2022年では年間259回実施されました。
抽せん方法
抽せん方法は数字の書かれた円盤を高速で回転させ、それに向かって矢を発射して刺さった場所の数字を並べたものが抽せん番号(当せん番号)になります。
ナンバーズ3
ナンバーズ3の抽せんで利用される円盤は下記の様なものです。(赤い矢印は回転方向です)
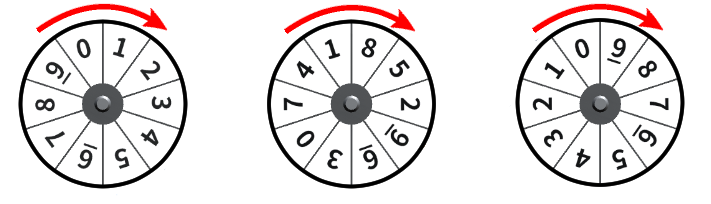
よく見るとそれぞれの円盤の数字の並びが異なりますね…。真ん中のリールは数字が3ずつずれたものになっています。
ナンバーズ4
ナンバーズ4の抽せんで利用される円盤は下記の様なものです。
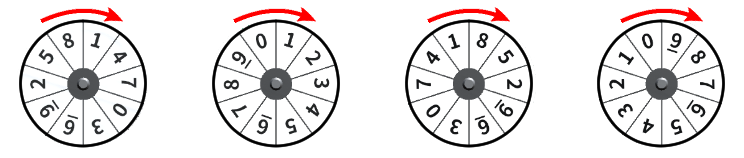
こちらも、円盤ごとに数字の並びが異なります。
また、右側3つはナンバーズ3の円盤の数字の並びが同じになります。これは抽せん会場によっては、ナンバーズ4の円盤の右3つを使ってナンバーズ3の抽せんを行う事があるためだと思います。
この円盤の並びを見ると、もし本命の数字が「333」とした時、「前後の2とか4も入れておいた方が…」と思った時に、円盤の数字を考えると、隣にくる「0」とか「6」を入れるみたいな考え方も浮かんできますが、そもそもどの数字が選ばれるか分からないので何とも言えないですね…。
数字の出現率
個人的な懸念点
抽せん方法で示したような円盤を回転させて矢で刺す方法で本当に数字は満遍なく選ばれるのでしょうか?
過去の出現率
2023年10月25日までの6327件の抽せん結果をもとに、各リールにおける「0」~「9」の数字が選択された割合を計算してみた結果以下の様になりました。
| 出現 数字 | ナンバーズ3 | ナンバーズ4 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 円盤 1 | 円盤 2 | 円盤 3 | 全体 | 円盤 1 | 円盤 2 | 円盤 3 | 円盤 4 | 全体 | |
| 0 | 9.72% | 10.29% | 9.82% | 9.94% | 9.97% | 10.12% | 10.72% | 9.83% | 10.16% |
| 1 | 9.91% | 9.80% | 9.97% | 9.89% | 9.51% | 10.08% | 9.78% | 10.48% | 9.97% |
| 2 | 10.08% | 9.93% | 10.34% | 10.12% | 10.21% | 8.49% | 9.09% | 10.16% | 9.49% |
| 3 | 10.07% | 10.51% | 9.74% | 10.10% | 9.96% | 10.46% | 10.07% | 9.66% | 10.04% |
| 4 | 9.96% | 10.21% | 9.70% | 9.96% | 9.97% | 9.58% | 9.86% | 9.75% | 9.79% |
| 5 | 8.99% | 9.83% | 9.93% | 9.58% | 9.51% | 10.61% | 10.00% | 10.08% | 10.05% |
| 6 | 10.45% | 9.53% | 9.39% | 9.79% | 10.57% | 9.61% | 9.40% | 9.74% | 9.83% |
| 7 | 9.80% | 9.99% | 10.15% | 9.98% | 10.05% | 10.29% | 10.13% | 9.59% | 10.02% |
| 8 | 10.19% | 9.61% | 10.59% | 10.13% | 10.29% | 10.05% | 10.15% | 9.91% | 10.10% |
| 9 | 10.83% | 10.31% | 10.38% | 10.51% | 9.94% | 10.72% | 10.80% | 10.80% | 10.56% |
どの円盤の数字もおおよそ10%=(1/10)になっています。
出現率にある程度偏りはありそうですが(試行回数が十分ではないためでしょう)、だからと言って「この数字は必ず来る」「この数字は必ず来ない」と言い切れるほどの差異はなさそうです。
ランダムになるのは円盤の初期位置や回転速度(変わっているのかな?)、矢の発射タイミングなどでこれだけばらつくのかな?と推測します。
乱数と見てよい?
抽せん数字が「0~9をランダムに並べたものか?」については、出現確率だけでは乱数に近いとは言い切れません…。(「000…000111…111222…222…….888…888999…9999」みたいに出現しても均等な出現率になってしまいますので)
ただ、各円盤の出現数字について、次の回ではどのような数字が出たか(例えば円盤1で「3」が出た次の回での円盤1の数字)の統計を取ると、やはり、0~9すべての数字が10%前後になるので、変な偏りはないのかなと思います。(検証結果は省略)
個人的な見解ですが、おそらく乱数と見てよいと思います。
抽せん数字の組み合わせ・当せん確率
ナンバーズでは、ストレート、ボックス、セット、ミニ(ナンバーズ3のみ)などの申し込み方法(購入方法)がありますが、それぞれについての抽せん数字の組み合わせ・当せん確率について見ていきたいと思います。
※以下の計算は特定の数字を買い続けるというものではなく、無作為に数字を選んだ場合の物になります。
ナンバーズ3
ナンバーズ3は「000」~「999」までの3桁の数字が抽せん数字となります。
ストレート(ナンバーズ3)
ストレートは各桁それぞれ0~9の10個の数字の中から一つずつ、合計3個選ぶ事になるので、組み合わせの数は下記になります。
組み合わせの数:10x10x10=1,000
抽せん数字は、この中の1つなので、当せん確率は下記になります。
当せん確率:(当せん数字数)÷(組み合わせ数)
=1÷1,000
=0.001
=0.1%
これは分かりやすいですね。
ボックス(ナンバーズ3)
ボックスも各桁それぞれ0~9の10個の数字の中から一つずつ、合計3個選ぶ事になりますが、各桁の数字を並び替えて抽せん数字と同じになれば当選となるのでやや複雑になります。
3桁すべて同じ数字
「111」の様に3桁すべて同じ数字になる場合は10通りありますが、並び替えても同じ数字になるので、ボックスで購入する事は出来ません…。
そのため、もし抽せん数字(当せん番号)がすべて同じ数字になった場合、ボックスで購入している数字はすべてハズレという事になります。
3桁すべての数字が異なる場合
「123」の様に各桁がすべて異なる数字は、1桁目は10個の数字から、2桁目は1桁目と異なる9個の数字から、3桁目は1桁目、2桁目とも異なる8個の数字から選択する事になるので、組み合わせの数は下記の通りになります。
組み合わせの数:10x9x8=720
「123」の様に各桁がすべて異なる数字が抽せんされた場合、下記の6つの数字が当せん番号となります。
「123」、「132」、「213」、「231」、「312」、「321」
これは並び替えの組み合わせ数なので、3x2x1=6という事になります。
当せん数字数:6
以上により、3桁すべての数字が異なる場合の当せん確率は以下の様になります。
当せん確率:(3桁すべて数字が異なる確率)x(当せん数字数)/(全組み合わせの数)
=(720/1000)x6/1000
=0.00432
=0.432%
3桁のうち2つの数字が同じ場合
「112」の様に3桁のうち2つの数字が同じ場合を考えます。
このような数字の組み合わせは、1桁目と2桁目が同じ場合(112)、1桁目と3桁目が同じ場合(121)、2桁目と3桁目が同じ場合(211)があります。
それぞれの場合、同じ数字は10個の数字から、残りは9個の数字から選択する事になるので、組み合わせの数は下記の通りになります。
組み合わせの数:(1桁目と2桁目が同じ場合の組み合わせ数)+(1桁目と3桁目が同じ場合場合の組み合わせ数)+(2桁目と3桁目が同じ場合の組み合わせ数)
=10x9+10x9+10x9
=270
また「112」の様に3桁のうち2つの数字が同じ数字が抽せんされた場合、下記の6つの数字が当せん番号となります。
「112」、「121」、「211」
これは同じ数字が2つある並び替えの組み合わせ数なので、3!/2!=3x2x1÷2=3という事になります。
当せん数字数:3
以上により、3桁のうち2つの数字が同じ場合の当せん確率は以下の様になります。
当せん確率:(3桁のうち2つの数字が同じになる確率)x(当せん数字数)/(全組み合わせの数)
=(270/1000)x3/1000
=0.00081
=0.081%
トータルの当せん確率(その1)
3桁の数字がすべて異なる数字になる場合と、3桁の数字の内2つが同じになる場合は、独立な事象(同時に起きるケースはない)なので、トータルの当せん確率は2つの場合の合計になります。
当せん確率:(各桁がすべて異なる場合の当せん確率)+(2つの数字が同じ場合の当せん確率)
=0.00432+0.00081
=0.00513
=0.513%
ボックスで申し込んだ場合、当せん確率はストレートの約5倍という事になります。
トータルの当せん確率(その2)
ボックス購入時の当せん確率は、別の考え方でも導き出す事が出来ます。
それは、必ずボックス当せんする数字の組み合わせの中から1つが選ばれるという考え方です。
3桁の数字がすべて異なる数字になる場合の数字の組み合わせは720通りでしたが、その場合6個ずつボックス当せんする数字の組み合わせが出来るので、その6個の中の1つさえ購入しておけば当せん数字がすべて数字が違う場合は当たります。
同じように3桁の数字の内2つが同じになる場合の組み合わせは270通りで、3組ずつボックス当せんする数字の組み合わせがあるので、その中の1つを購入すれば、当せん数字が、同じ数字が2つ含まれる場合は当たります。
そのため当せん番号がすべて同じ数字でない場合は、(720)/6 +(270)/3通りの数字をすべて購入すれば、どれかは当たるはずです。
当せん確率:1÷((各桁がすべて異なる場合の当せん数字組み合わせ数)+(2つの数字が同じ場合の当せん数字組み合わせ数)
=1÷((720)/6+(270)/3)
=1÷(120+90)
=1÷210
=0.00476
=0.476%
しかし、当せん番号がすべて同じ数字の時には「ハズレ」てしまうので、その分を考慮します。
当せん確率(改)=(すべて同じ数字を除いた)当せん確率x(すべて数字が同じにならない組み合わせ/すべての組み合わせ)
=0.00476x(990/10,000)
≒0.00471
=0.471%
こちらの計算方法を使うとボックスで申し込むと当せん確率は、ストレートの約5倍弱という事になります。
2種類の当せん確率が出てしまいました。どちらが正しいのでしょう???(自分も最初の内は混乱しました。どっちもあってそうだけど、数字が合わないと…)
セット(ナンバーズ3)
セット購入の場合、購入時にはストレート・ボックスの区別なく、抽せん結果によって当せんが振り分けられます。
例えば「123」をセットで購入した場合、
抽せん数字が「123」の場合:ストレート当せん
抽せん数字が「132」「213」「231」「312」「321」の場合:ボックス当せん
となります。
「ストレートもしくはボックス」が当たる可能性はボックスの時と同じなので、0.513%もしくは0.471%となります。
セットのストレートは、セットでないストレート当せん確率0.1%と言いたい所ですが、すべて同じ数字はセットでは選択できないので、990/1000を掛けた値になるでしょう。
セットの場合ストレートとボックスは同時には当せんしないので、セットのボックスの当せん確率は全体の確率からストレートの確率を減じたものになるはずです。
セット:ストレートの当せん確率:0.099%
セット:ボックスの当せん確率:0.414 or 0.372%(?)
※当せん確率が2種類あるのは気持ち悪いかも知れませんがご容赦下さい。
ミニ(ナンバーズ3)
ミニは2桁の数字を選択するので、各桁それぞれ0~9の10個の数字の中から一つずつ、合計2個選ぶ事になるので、組み合わせの数は下記になります。
組み合わせの数:10x10=100
抽せん数字は、この中の1つなので、当せん確率は下記になります。
当せん確率:1÷100=0.01=1%
こちらは非常に明快ですね…^^;
組み合わせ数の検証
これまで記載した組み合わせ数が正しいかを、ナンバーズ3のこれまでの6327回分の抽せん結果で確認してみます。
| 抽せん数字の種類 | 出現回数 | 出現割合 |
|---|---|---|
| 数字がすべて同じ(例:「111」) | 52 | 0.8% |
| 数字がすべて異なる(例:「123」) | 4530 | 71.6% |
| 2つの数字が同じ(例:「112」) | 1745 | 27.6% |
| 合計 | 6327 | 100% |
やや2つの数字が同じ場合が多めですが、おおよそ想定通りの値ですね。
ナンバーズ4
ナンバーズ4は「0000」~「9999」までの4桁の数字が抽せん数字となります。
ストレート(ナンバーズ4)
ストレートは各桁それぞれ0~9の10個の数字の中から一つずつ、合計4個選ぶ事になるので、組み合わせの数は下記になります。
組み合わせの数:10x10x10x10=10,000
抽せん数字は、この中の1つなので、当せん確率は下記になります。
当せん確率:(当せん数字数)÷(組み合わせ数)
=1÷10,000
=0.0001
=0.01%
ボックス(ナンバーズ4)
ボックスも各桁それぞれ0~9の10個の数字の中から一つずつ合計4個選ぶ事になりますが、各桁の数字を並び替えて抽せん数字と同じになれば当選となります。
組み合わせや確率の計算はナンバーズ3の時よりもう少し複雑になりますが、考え方は同じです。
4桁すべて同じ数字
「1111」の様に4桁すべて同じ数字になる場合は10通りありますが、並び替えても同じ数字なので、ボックスで購入する事は出来ません…。
すべての数字が異なる場合
「1234」の様に各桁がすべて異なる数字は、1桁目は10個の数字から、2桁目は1桁目と異なる9個の数字から、3桁目は1桁目、2桁目とも異なる8個の数字から、4桁目はどれとも被らない7個の数字から選択する事になるので、組み合わせの数は下記の通りになります。
組み合わせの数:10x9x8x7=5,040
「1234」の様に各桁がすべて異なる数字が抽せんされた場合、下記の24個の数字が当せん番号となります。
「1234」、「1243」、「1324」、「1342」、「1423」、「1432」、
「2134」、「2143」、「2314」、「2341」、「2413」、「2431」、
「3124」、「3142」、「3214」、「3241」、「3412」、「3421」、
「4123」、「4132」、「4213」、「4231」、「4312」、「4321」、
これは並び替えの組み合わせ数なので、4x3x2x1=24という事になります。
当せん数字数:24
以上により、4桁すべての数字が異なる場合の当せん確率は以下の様になります。
当せん確率:(4桁すべて数字が異なる確率)x(当せん数字数)/(全組み合わせの数)
=(5,040/10,000)x24/10,000
≒0.00121
=0.121%
2つの数字が同じで残りもバラバラな場合
「1123」の様に4桁のうち2つの数字が同じで残りの2つの数字がバラバラな場合を考えます。
このような数字の組み合わせは、1桁目と2桁目が同じ場合(1123)、1桁目と3桁目が同じ場合(1213)、1桁目と4桁目が同じ場合(1231)、2桁目と3桁目が同じ場合(2113)、2桁目と4桁目が同じ場合(2131)、3桁目と4桁目が同じ場合(2311)の6通りがあります。
それぞれの場合で、同じ数字は10個の数字から、残りはそれぞれ9個、8個の数字から選択する事になるので、組み合わせの数は下記の通りになります。
組み合わせの数:(10x9x8)x6
=4,320
また「1123」の様に4桁のうち2つの数字が同じで残りの2つの数字がバラバラな数字が抽せんされた場合、下記の6つの数字が当せん番号となります。
「1123」、「1132」、「1213」、「1231」、「1312」、「1321」
「2113」、「2131」、「2311」、「3112」、「3121」、「3211」
これは4つの数字の中に同じ数字が2つある並び替えの組み合わせ数なので、4!/2!=4x3x2x1÷2=12という事になります。
当せん数字数:12
以上により、4桁のうち2つの数字が同じで残りの2つの数字がバラバラな場合の当せん確率は以下の様になります。
当せん確率:(4桁のうち2つの数字が同じで残りの2つの数字がバラバラな場合の確率)x(当せん数字数)/(全組み合わせの数)
=(4,320/10,000)x12/10,000
≒0.00052
=0.052%
2つの同じ数字の組み合わせになる場合
「1122」の様に4桁のうち2つの同じ数字の組み合わせになる場合を考えます。
このような数字の組み合わせは、1桁目と2桁目が同じ場合(1122)、1桁目と3桁目が同じ場合(1212)、1桁目と4桁目が同じ場合(1221)の3通りがあります。(数字を入れ替えても同じになる「1122」「2211」は同じとみなせるため)
それぞれの場合で、10個の数字から、重複しない2個の数字を選択する事になるので、組み合わせの数は下記の通りになります。
組み合わせの数:(10x9)x3
=270
また「1122」の様に4桁のうち2つの同じ数字の組み合わせの数字が抽せんされた場合、下記の6つの数字が当せん番号となります。
「1122」、「1212」、「1221」、「2112」、「2121」、「2211」
これは4つの数字の中に同じ数字が2つずつある並び替えの組み合わせ数なので、4!/(2!x2!)=4x3x2x1÷(2x2)=6という事になります。
当せん数字数:6
以上により、4桁のうち2つの同じ数字の組み合わせになる場合の当せん確率は以下の様になります。
当せん確率:(4桁のうち2つの同じ数字の組み合わせになる場合の確率)x(当せん数字数)/(全組み合わせの数)
=(270/10,000)x6/10,000
≒0.000016
=0.0016%
3つの数字が同じ場合
「1112」の様に4桁のうち3つの数字が同じ場合を考えます。
このような数字の組み合わせは、1、2、3桁目が同じ場合(1112)、1、2、4桁目が同じ場合(1121)、1、3、4桁目が同じ場合(1211)、2、3、4桁目が同じ場合(2111)の4通りがあります。
それぞれの場合で、同じ数字は10個の数字から、残りは9個の数字から選択する事になるので、組み合わせの数は下記の通りになります。
組み合わせの数:(10x9)x4
=360
また「1112」の様に4桁のうち3つの数字が同じ数字が抽せんされた場合、下記の4つの数字が当せん番号となります。
「1112」、「121」、「1211」、「2111」
これは4つの数字の中に同じ数字が3つある時の並び替えの組み合わせ数なので、4!/3!=4x3x2x1÷(3x2x1)=4という事になります。
当せん数字数:4
以上により、4桁のうち3つの数字が同じになる場合の当せん確率は以下の様になります。
当せん確率:(4桁のうち3つの数字が同じになる場合の確率)x(当せん数字数)/(全組み合わせの数)
=(360/10,000)x4/10,000
≒0.000014
=0.0014%
トータルの当選確率(その1)
各桁がすべて異なる場合、2つの数字が同じでその他はバラバラな場合、2つの同じ数字の組み合わせの場合、3つの数字が同じ場合というのはそれぞれ独立な事象なので、ボックス購入時の当せん確率は、それぞれの場合の当せん確率を合計すれば良いので、以下の様になります。
当せん確率:1÷((4桁のうちすべての数字が異なる場合の当せん確率)+(2つの数字が同じで残りもバラバラな場合の当せん確率)+(2つの同じ数字の組み合わせになる場合の当せん確率)+(3つの数字が同じ場合の当せん確率)
=0.00121+0.00052+0.000016+0.000014
=0.00176
=0.176%
ボックスで申し込むと当せん確率は、ストレートの約17倍という事になります。
トータルの当選確率(その2)
ナンバーズ3の時と同様にもう一つの考え方で当せん確率を計算してみます。
ボックス購入時の当せん確率は、当せん数字のすべての組み合わせを購入すれば、その内の1つは当せんする事になるので、以下の様になります。
当せん確率:1÷((各桁がすべて異なる場合の当せん数字組み合わせ数)+(2つの数字が同じで残りがバラバラな場合の当せん数字組み合わせ数)+(2つの同じ数字の組み合わせになる場合の当せん数字組み合わせ数)+(3つの数字が同じ場合の当せん数字組み合わせ数)
=1÷(5,040/24+4,320/12+270/6+360/4)
=1÷(210+360+45+90)
=1÷705
≒0.00142
=0.142%
しかし、当せん番号がすべて同じ数字の時には「ハズレ」てしまうので、その分を考慮します。
当せん確率(改)=(すべて同じ数字を除いた)当せん確率x(すべて数字が同じにならない組み合わせ/すべての組み合わせ)
=0.00142x(9,990/10,000)
≒0.00142
=0.142%
こちらの計算ではボックスで申し込むと当せん確率は、ストレートの約14倍という事になります。
セット(ナンバーズ4)
セット購入の場合、購入時にはストレート・ボックスの区別なく、抽せん結果によって当せんが振り分けられます。
例えば「1234」をセットで購入した場合、
抽せん数字が「1234」の場合:ストレート当せん
抽せん数字が「1243」「1324」「1342」「1423」「1432」「2134」「2143」「2314」「2341」「2413」「2431」「3124」「3142」「3214」「3241」「3412」「3421」「4123」「4132」「4213」「4231」「4312」「4321」の場合:ボックス当せん
となります。
「ストレートもしくはボックス」が当たる可能性はボックスの時と同じなので、0.176%もしくは0.142%となります。
セットのストレートは、セットでないストレート当せん確率0.01%と同じになりそうですが、すべて同じ数字はセットでは選択できないので、9990/10000を乗じた値になるでしょう(ほぼ1を掛ける事になるので、結果はほぼ変わりませんが…)。
セットの場合ストレートとボックスは同時には当せんしないので、セットのボックスの当せん確率は全体の確率からストレートの確率を減じたものになるはずです。
セット:ストレートの当せん確率:0.01%
セット:ボックスの当せん確率:0.166 or 0.132%(?)
※当せん確率が2種類あるのは気持ち悪いかも知れませんがご容赦下さい。
組み合わせ数の検証
これまで記載した組み合わせ数が正しいかを、ナンバーズ4のこれまでの6327回分の抽せん結果で確認してみます。
| 抽せん数字の種類 | 出現回数 | 出現割合 |
|---|---|---|
| 数字がすべて同じ(例:「1111」) | 6 | 0.09% |
| 数字がすべて異なる(例:「1234」) | 3225 | 50.97% |
| 2つの数字が同じで他は異なる(例:「1123」) | 2710 | 42.83% |
| 同じ数字の2つの組み合わせ(例:「1122」) | 148 | 2.34% |
| 3つの数字が同じ(例:「1112」 | 238 | 3.76% |
| 合計 | 6327 | 100% |
ナンバーズ4については試行回数が6327回だとちょっと少ないと思いますが、おおよそ想定通りの値ですね。
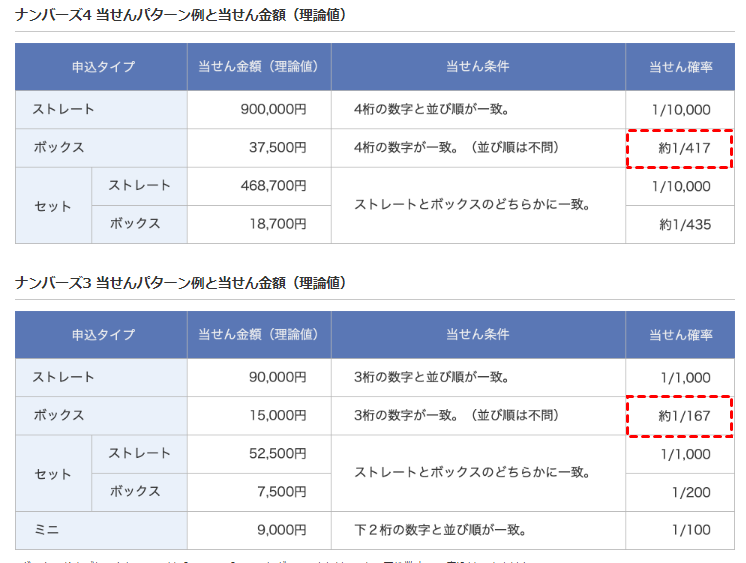
当せん確率まとめ
当せん確率をまとめると下記の様になります。
| くじ種別 | 申込種別 | 当せん確率(1/X) | 当せん確率(%) |
|---|---|---|---|
| ナンバーズ3 | ストレート | 1/1,000 | 0.1% |
| ボックス | 約1/195 | 0.513% | |
| 約1/212 | 0.471% | ||
| セット(ストレート) | 約1/1,010 | 0.099% | |
| セット(ボックス) | 約1/242 | 0.414% | |
| 約1/266 | 0.376% | ||
| ミニ | 1/100 | 1% | |
| ナンバーズ4 | ストレート | 1/10,000 | 0.01% |
| ボックス | 約1/568 | 0.176% | |
| 約1/705 | 0.142% | ||
| セット(ストレート) | 約1/10,010 | 0.01% | |
| セット(ボックス) | 約1/602 | 0.166% | |
| 約1/757 | 0.132% |
※ボックスの確率が2つあるのはご容赦ください。
※どちらにしても、みずほ銀行の「ナンバーズ」の紹介ページのボックスの当せん確率が異なりますが、そっちの方は確率が高過ぎるのでは…?と思います。すべて異なる数字のケースしか考慮されていない様な気がします…。
https://www.mizuhobank.co.jp/retail/takarakuji/products/numbers/index.htmlより引用
当せん金
ナンバーズ宝くじの当せん金について見てみたいと思います。
統計データ
自分で確認できる範囲で当せん金の最小値・最大値・平均値を求めると下記の様になりました。
※調べられた範囲は2022年10月以降分です。それ以前は分かりませんでした…。
ナンバーズ3の当せん金
| 申込種別 | 最小値(円) | 最大値(円) | 平均値(円) |
|---|---|---|---|
| ストレート | 41,200 円 | 132,400 円 | 90,451 円 |
| ボックス | 8,400 円 | 43,400 円 | 19,532 円 |
| セットーストレート | 27,400 円 | 86,800 円 | 55,008 円 |
| セットーボックス | 4,200 円 | 21,700 円 | 9,740 円 |
| ミニ | 4,100 円 | 13,200 円 | 9,000 円 |
ナンバーズ4の当せん金
| 申込種別 | 最小値(円) | 最大値(円) | 平均値(円) |
|---|---|---|---|
| ストレート | 126,900 円 | 1,641,800 円 | 906,073 円 |
| ボックス | 10,500 円 | 291,000 円 | 61,331 円 |
| セットーストレート | 68,700 円 | 889,300 円 | 483,679 円 |
| セットーボックス | 5,200 円 | 145,500 円 | 30,640 円 |
当せん金の妥当性検証
当せん金はその回の販売実績や当せん口数の大小によってばらつきが出てしまうものです。
しかし、平均値を見ればおよそ理論値に近い値にはなると思いますので、平均値から当せん金の妥当性を見てみます。
回収率について(トータルの当せん確率(その2)ベース)
それぞれくじについて、ストレート・ボックスの申し込み方法(購入方法)で、必ず当たる様に全通り1口(200円)ずつ購入した時の購入金額、当せん金額、回収率を列挙してみます。
| くじ種別 | 申込種別 | 必ず当たる 組み合わせ数 | 全通り購入時 金額(円) | 平均当せん 金額(円) | 回収率 |
|---|---|---|---|---|---|
| ナンバーズ3 | ストレート | 1,000 | 200,000 円 | 90,451 円 | 0.452 |
| ボックス | 210 | 42,000 円 | 19,532 円 | 0.465 | |
| ミニ | 100 | 20,000 円 | 9,000 円 | 0.45 | |
| ナンバーズ4 | ストレート | 10,000 | 2,000,000 円 | 906,073 円 | 0.453 |
| ボックス | 705 | 141,000 円 | 61,331 円 | 0.435 |
回収率はどれもおよそ「0.45」に近い値になっています。
この値は、くじの販売額に対する当せん金に割り当てらる割合(45%)に相当します。
なので、回収率からみて当せん金額は妥当の様に思えます。
あれ?でも、上記の表は「トータルの当せん確率(その2)」で確率を求めた様に必ず当たる組み合わせをすべて買ったものと同じになります。
では、当せん確率は、「トータルの当せん確率(その2)」の方が正しいのでしょうか?
シミュレーションによる当せん確率のチェック
試行回数を稼ぐために実際のナンバーズの結果ではなく、乱数生成器で選択数字、抽選数字を生成して、それぞれの当せん確率をシミュレーションしてみました。
※試行回数は100万回です。
| くじ種別 | 申込種別 | シミュレーション上の 当せん確率(%) |
|---|---|---|
| ナンバーズ3 | ストレート | 0.10% |
| ボックス | 0.508% | |
| セット:ストレート | 0.098% | |
| セット:ボックス | 0.414% | |
| ミニ | 1.000% | |
| ナンバーズ4 | ストレート | 0.012% |
| ボックス | 0.176% | |
| セット:ストレート | 0.012% | |
| セット:ボックス | 0.164% |
シミュレーションでは、ボックスの当せん確率は「トータルの当せん確率(その1)」に近くなります。
回収率について(トータルの当せん確率(その1)ベース)
「トータルの当せん確率(その1)」ベース考える場合は、ナンバーズ3は000~999を、ナンバーズ4は0000~9999をすべての申し込み種別で購入した時の当せん金を計算してみます。
ただし、ボックスではすべて同じ数字の並びは購入できませんので、それを考慮します。
当選金額は、購入組み合わせ数*当せん確率*平均当せん金額で求めています。
| くじ種別 | 申込種別 | 購入可能な重複 しない組み合わせ | 全通り購入時 金額(円) | 当せん金額 (円) | 回収率 |
|---|---|---|---|---|---|
| ナンバーズ3 | ストレート | 1,000 | 200,000 円 | 90,451 円 | 0.452 |
| ボックス | 990 | 198,000 円 | 99,197 円 | 0.501 | |
| ミニ | 100 | 20,000 円 | 9,000 円 | 0.45 | |
| ナンバーズ4 | ストレート | 10,000 | 2,000,000 円 | 906,073 円 | 0.453 |
| ボックス | 9,990 | 1,998,000 円 | 1,078,346 円 | 0.540 |
こっちの確率をベースにすると、ボックスの回収率が0.45をを大きく超えてしまいます。
回別の総当せん金/販売額が45%を超える事はないので、多分この数字・考え方は間違っているのでしょう…
しかし、シミュレーション上の当せん確率はあっているんだけどなぁ…う~ん…?
くじ種別・申込種別の比較
くじ種別・申込種別で損得があるかを確認してみます。
ナンバーズ3とナンバーズ4
ストレート、ボックスの当せん金額(平均)を並べてみると下記の様になります。
| ナンバーズ3 | ナンバーズ4 | 当せん金倍率 | |
|---|---|---|---|
| ストレート | 90,451 円 | 906,073 円 | 10.02倍 |
| ボックス | 19,532 円 | 61,331 円 | 3.14倍 |
ナンバーズ4のストレートの当せん金額はナンバーズ3に比べて約10倍になります。
これは確率として1/10当たりにくいので、当せん金が10倍になるのは、何となく直感的に分かります。
ただ、ナンバーズ4のボックス当せん金はナンバーズ3のそれに比べて10倍にはなっていませんが、これは、ボックスの当せん確率を比べると分かります
| ナンバーズ3 | ナンバーズ4 | 当せん確率倍率 の逆数 | |
|---|---|---|---|
| ストレート | 1/1,000 | 1/10,000 | 10倍 |
| ボックス | 1/212 | 1/705 | 3.32倍 |
当せん確率の比率から見ると、ボックス当せん金が3.32倍程度になるのが妥当なのが分かります。
ただ、現状3.14倍(円周率みない…)と若干低いのは、試行回数が少ないためでしょう…。
(ナンバーズ4は10,000通りあるのに対して、まだ6,300回程度しか実施されてませんので…。)
セットとセットでない場合
セットで購入すると完全一致でストレート、数字の並び替えであってればボックスとして当せんします。
これはセットでないストレートとボックスを合わせて購入する場合に比べるとどうなのかを平均当せん金額を並べて比較してみます。
| くじ種別 | 申込種別 | セット 当せん金額 | セットでない 当せん金額 | 当せん金の 倍率 |
|---|---|---|---|---|
| ナンバーズ3 | ストレート | 55,008 円 | 90,451 円 | 1.644 倍 |
| ボックス | 9,740 円 | 19,532 円 | 2.005 倍 | |
| ナンバーズ4 | ストレート | 483,679 円 | 906,073 円 | 1.873 倍 |
| ボックス | 30,640 円 | 61,331 円 | 2.002 倍 |
ボックスは2倍でどちらを買っても同じようですが、ストレートは一見してセットで購入した方がお得に見えます。
これはセット購入の仕組みによるものです。
セットは0.5口(100円)でストレート、0.5口(100円)でボックスをセットで購入していると言ってよいでしょう。その場合ストレートで当たるという事は、同時にボックスで当たっている事になるので、そのボックス当せん分の当せん金がストレートの当せん金に上乗せされている事になります。
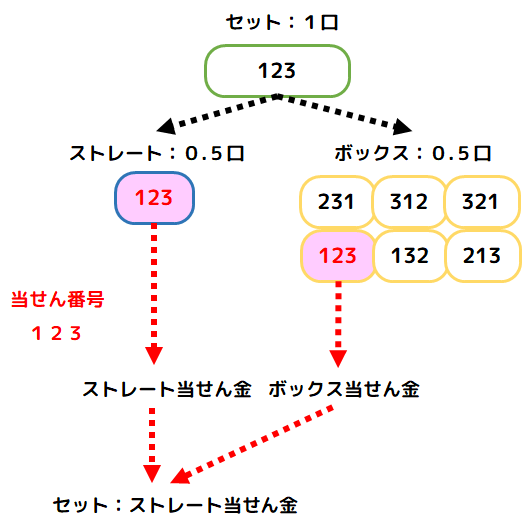
これは、同じ数字でセットでないストレートとセットでないボックスを1口ずつ購入したのと同じになります。
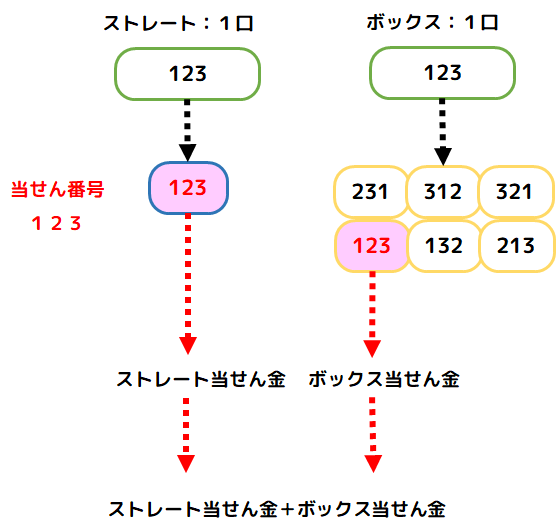
なので、セットでないストレートにボックスの当せん金を加算して比較すると…
| くじ種別 | 申込種別 | セット 当せん金額 | セットでない 当せん金額 | ストレート + セット | 当せん金の 倍率 |
|---|---|---|---|---|---|
| ナンバーズ3 | ストレート | 55,008 円 | 90,451 円 | 109,983 円 | 1.999 倍 |
| ボックス | 19,532 円 | ||||
| ナンバーズ4 | ストレート | 483,679 円 | 906,073 円 | 967,404 円 | 2.000 倍 |
| ボックス | 30,640 円 | 61,331 円 |
結論としては、購入金額の差(比)そのものになるので、セットもセットでない場合も特段に差はありませんね…。
セットで買うとお手軽と言う点はありますが。
ナンバーズ3のミニとセットボックス
普段ナンバーズ3のミニとセットボックスの当せん金を見ていると下記の様に、ミニの当せん金の方が多いような気がします。
| 抽せん回 | 第6326回 |
| ナンバーズ3:セットーボックス当せん金 | 6,400円 |
| ナンバーズ3:ミニ当せん金 | 7,600円 |
しかし、全体の平均を見るとミニの9,000円に対してセットボックスの方が9,740円とやや上回っています。
これはセットで購入する数字によるものです。
例えば「123」の様にすべて違う数字を買うとすると、ボックス当せん数は6通り存在するので、当せん確率はストレートの6倍になりますが、当然当せん金額はストレートの約1/6になります。
ストレートの平均当せん金が約9万円とすると、ボックス当せん金の平均は1万5千円、さらにセットの場合0.5口分になるので、7千5百円が平均当せん金額になるので、当然ミニの9,000円よりは下がってしまいます。
全体のセットボックスの平均当せん金額を押し上げているのは、「112」の様に同じ数字が2つ含まれている場合です。こちらのボックス当せん数は3通り存在するので、当せん確率はストレートの3倍になり、当せん金額はストレートの約1/3になります。理論上1万5千円の平均当せん金額になり、ミニの9千円より多くなります。
ミニの当せん金額が大きいケースを良く目にするのは、「123」の様にすべて違う数字で成り立つ場合が全体の72%なので、出現率が多いためですね。
※ミニの当せん確率は1%ですが、セットの場合0.1%の確率でセットストレートが当せんする確率があり、それが当たれば当然セット購入の方がミニの何倍も当せん金額が増えます。(当たればですけど…)
必勝法は存在する?
たまぁに、『ナンバーズ必勝法』という言葉を聞いたりしますが、抽せん数字(当せん番号)は予測可能なのでしょうか?
必勝法は存在しない(個人的意見)
一様乱数の数字の並びから次に出現する数字を予測する事が出来ない様に、ナンバーズの次の数字を予測する事は出来ないでしょう。
それは、コインの裏表を完璧に予測するような物ですが、そのような事は出来ません…(参考:「確率:コインの裏表」)
試行回数が少ないと、出現数字に偏りが出る場合があります。
そのため『次もこの数字が出る流れだ』とか『次はこの数字以外が来る!』と言う事と言って、その通りになる事もありますが、それはたまたまです…。
必勝法がもし存在したら?
もし、必勝法が存在したらどうなるでしょうか?
次にくる抽せん数字は必ず「777」と分かったとして、その数字を全員が選んだとしたら、もし当せんしても、当せん金額は1口90円になるでしょう…。(まぁ、僕の様なひねくれものが「777」以外を購入するので、数円は当せん金額が上がるかも知れませんが…)
そして、もし本当に必勝法があったとしたら、それは他人には言わないでしょう…。なぜなら当せん金は、当せん口数が多ければそれに反比例して少なくなってしまうからです。
『必勝法』を売る商売があるという事は、逆に言えば必勝法が無いからだともいえるでしょう…。
どういう買い方が良いのか?
期待値はどれも同じ
これまで見てきた様に購入総口数(総金額)に対する当せん金額の期待値は、ナンバーズ3,ナンバーズ4もどの申し込み方法でも45%と同じでした。
何万口、何十万口と買っていけば、どれも同じ様な収支に収束していきます…。(収束するほどの口数を買うのは相当大変でしょうけど…)
違うのは、当せん確率と、当せん金額です。
なので、手堅く確率の高いミニを買い続けるのも良し、一発狙いでストレートを買い続けるのも良し、中間のボックスを狙うのも良しだと思います。
狙い目は?
この記事では、基本無作為に数字を選択するという事を前提にしてきましたが、ナンバーズでは、当せん口数・当せん金額が変動します。
人気のある(申込口数の多い)数字で当せんすると、当せん口数が多くなり、そのため当せん額が減ります。
※ナンバーズ4のストレートの最小当せん金額は12万程度で、もし当たってもちょっと残念な気になるかもしれません。
なので、人気のない(申込口数が少ない)数字を買い続けると良いかも知れません。(ただ、どの数字が人気がないかは難しい所ではありますが…)
シミュレーションしてみると
実データではなく、乱数で選択数字、抽選数字を生成し、当せん金額はいつも平均だとして、ストレート、ボックス、ミニを1口ずつ購入し続けた時の回収率の一例を下記に示します。
※シミュレーションの一例で必ずこのようになるとは限りません…。
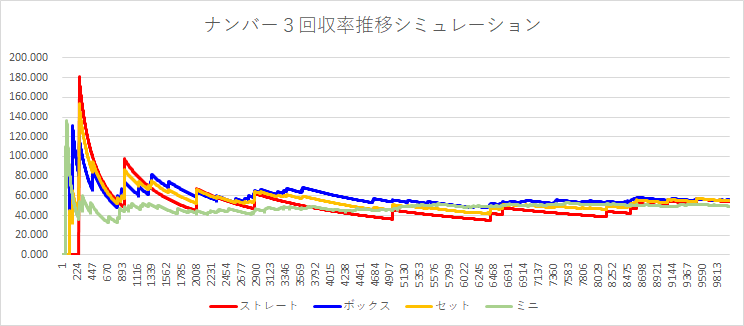
どれを買っても1万回後には回収率が45~50%あたりに収束してしまいます。
グラフを見ると、どれも最初の方にピークがありますが、これは、最初の方で何回か当せんするツイてる方のデータです。
別のシミュレーションでは以下の様にミニ以外一度も回収率100%を超えなかったものもあります。
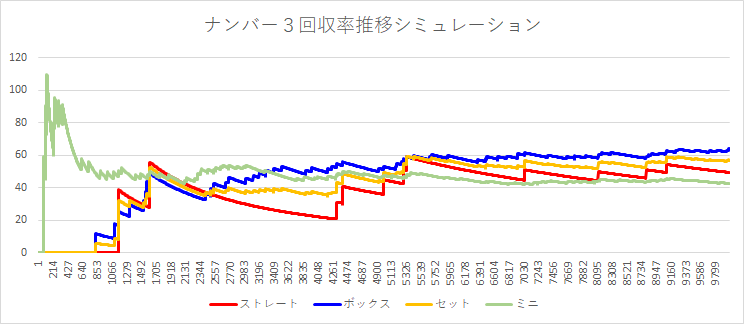
シミュレーションを見る限り、くじを始めて、一度大当たりしたり、回収率が100%を超えたりしたら、そこで止めるのが良いような気もします。
ただ、それが出来ないんですけど…^^;
『次は当たるかも』『次も当たるかも』という根拠のない自信が理屈に勝ってしまう…^^;
まとめ
今回は、自分が好きなナンバーズについて、組み合わせや確率を見てきました。
ナンバーズの抽せん数字は一様乱数に従っている様なので、確率に従っていると言えるでしょう。
まぁ、当たるも八卦、当たらぬも八卦、楽しくやるのが一番ですね。
コメント